What is Surface Area of Cone? Formula, Examples, and Easy Guide

Introduction

If you’ve ever looked at an ice cream cone, a party hat, or a funnel, you’ve seen a cone in action. But have you ever wondered how much material it would take to wrap or paint the outside of that cone? That’s where the surface area of a cone comes in.

While the volume of a cone tells us how much it can hold inside, the surface area tells us how much space its outer covering takes up. This measurement is useful in geometry, engineering, architecture, and even in daily life.

In this article, we’ll explore what the surface area of a cone is, the formulas you need, step-by-step calculations, common mistakes, and real-world applications. By the end, you’ll have a clear understanding and plenty of practice examples to work with.

What is a Cone?

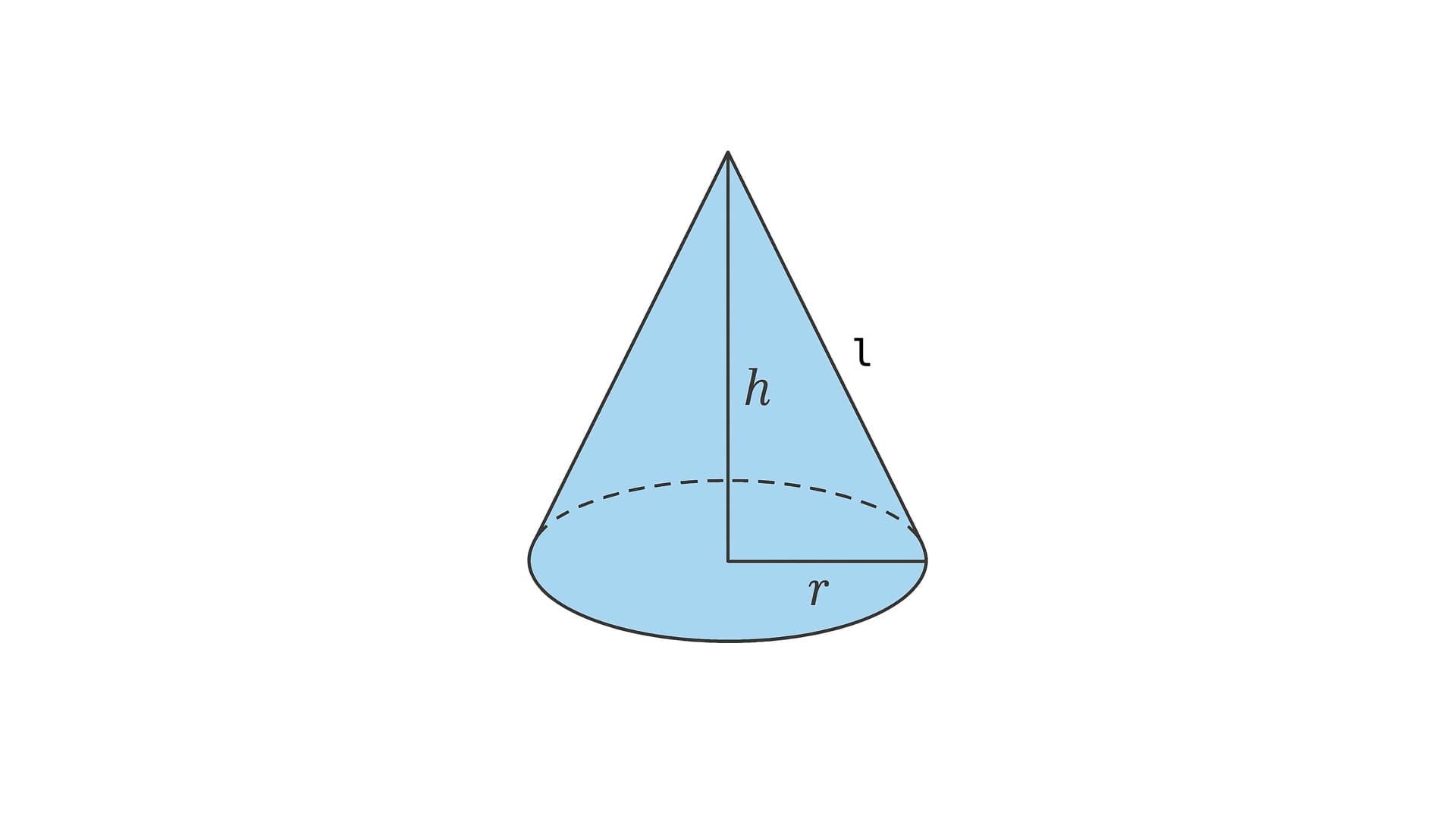
A cone is a three-dimensional shape that has:

A circular base
An apex (vertex), a single point above the base
A height (h), which is the perpendicular distance from the apex to the base
A radius (r), the distance from the center of the base to its edge
A slant height (l), which is the diagonal distance from the apex to a point on the circular edge

Key difference: For volume, we only need height (h). For surface area, we need the slant height (l).

Real-life examples of cones:

Ice cream cone
Funnel
Traffic cone
Party hat
Rocket nose cone
Pointed tents

Surface Area of a Cone Explained

The surface area of a cone is the total area of its outside covering. It consists of two parts:

Curved Surface Area (CSA): The area of the cone’s curved side.
- Formula: CSA = πrl
Base Area: The area of the circular base.
- Formula: Base = πr²
Total Surface Area (TSA): The sum of CSA and Base Area.
- Formula: TSA = πrl + πr² = πr(l + r)

Where:

r = radius of the base
l = slant height of the cone

The slant height (l) can be found using the Pythagoras theorem if you know height and radius: l = √(r² + h²)

Step-by-Step Calculation

Let’s walk through a couple of worked examples.

Example 1: Small Cone

A cone has a radius of 3 cm and a slant height of 5 cm. Find its curved and total surface area.

Step 1: Write the formulas

CSA = πrl

TSA = πrl + πr²

Step 2: Plug in values

CSA = 3.14159 × 3 × 5 = 47.12 cm²

TSA = 47.12 + 3.14159 × 9 = 47.12 + 28.27 = 75.39 cm²

Answer:

Curved surface area = 47.12 cm²
Total surface area = 75.39 cm²

Example 2: Traffic Cone

A traffic cone has a radius of 7 inches and a slant height of 25 inches. Find its total surface area.

Step 1: TSA = πr(l + r)

Step 2: TSA = 3.14159 × 7 × (25 + 7)

Step 3: TSA = 3.14159 × 7 × 32 = 703.72 in²

Answer: The cone’s total surface area is 703.72 square inches.

Example 3: Using Height Instead of Slant Height

A cone has a height of 12 cm and a radius of 9 cm. Find its TSA.

Step 1: Find slant height using Pythagoras:

l = √(r² + h²) = √(9² + 12²) = √(81 + 144) = √225 = 15 cm

Step 2: TSA = πr(l + r)

= 3.14159 × 9 × (15 + 9)

= 3.14159 × 9 × 24

= 678.58 cm²

Answer: TSA = 678.58 cm²

Common Mistakes Students Make

Mixing up height and slant height → Always use slant height for surface area.
Forgetting the base area → If asked for TSA, add πr² as well.
Rounding too early → Keep π as 3.14159 until the final step.
Using diameter instead of radius → Remember radius = diameter ÷ 2.

Cone Surface Area vs Volume

It’s easy to confuse surface area and volume, so here’s a quick comparison:

Surface Area (TSA): πr(l + r) → measures outer covering.
Volume: (1/3)πr²h → measures inside capacity.

Example: A party hat.

Volume tells you how much space is inside (air inside the hat).
Surface area tells you how much cardboard or paper is needed to make it.

FAQs About Cone Surface Area

1. What is the formula for curved surface area of a cone?

CSA = πrl

2. What is the formula for total surface area of a cone?

TSA = πr(l + r)

3. What’s the difference between CSA and TSA?

CSA includes only the curved outside, while TSA includes both curved surface and base area.

4. Why is slant height used in surface area?

Because the cone’s side is a slanted triangle, not vertical height.

5. Can I use diameter instead of radius?

Yes, but divide it by 2 before plugging into the formula.

6. What units are used for surface area?

Always square units: cm², m², in², etc.

7. Is surface area used in real life?

Yes — from designing hats to calculating paint for cone-shaped structures.

Conclusion

The surface area of a cone tells us how much material is needed to cover it. The key formulas are:

Curved Surface Area (CSA) = πrl
Total Surface Area (TSA) = πr(l + r)

Remember to always use the slant height when working with surface area, and add the base area when asked for TSA. From ice cream cones to rocket tips, this simple geometry concept has wide applications in real life.

Next time you see a cone, you’ll know not just how much it can hold, but also how much material it would take to wrap it!