Introduction
Have you ever looked at an ice cream cone and wondered how much ice cream it can actually hold? Or maybe you’ve been asked in math class, “What is the volume of a cone?” Understanding this simple but important geometry concept opens the door to solving real-life problems in design, construction, and everyday situations.
In this article, we’ll break down everything you need to know about cone volume. From the basic formula to step-by-step calculations and real-world applications, you’ll leave with a solid grasp of the topic.
What is a Cone?
Before diving into the math, let’s understand the shape itself.
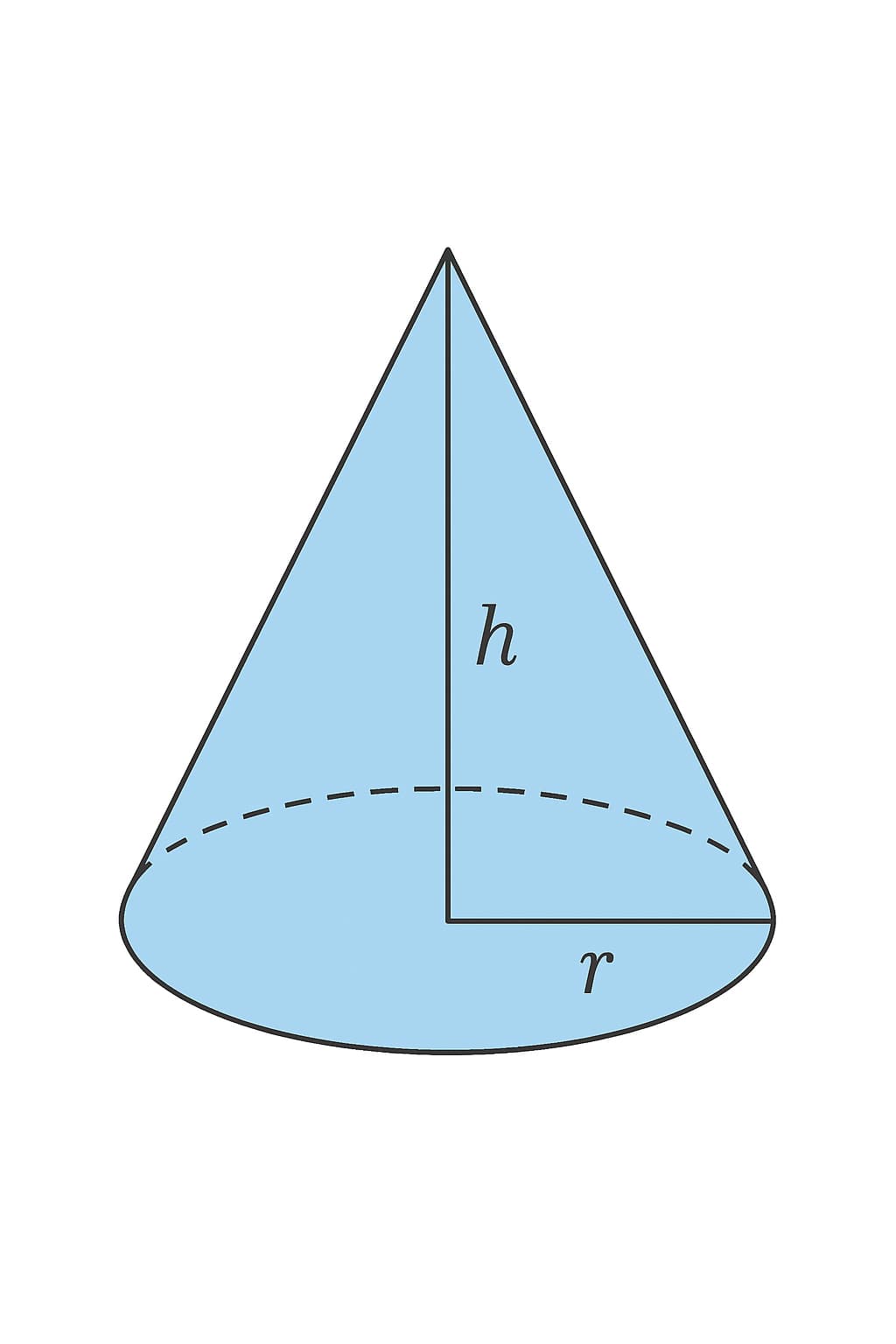
A cone is a three-dimensional (3D) geometric shape with two main parts:
- A circular base
- A single point at the top (called the apex or vertex)
The line that runs from the apex straight down to the center of the base is the height (h) of the cone. The distance from the center of the base to its edge is the radius (r).
Everyday Examples of Cones
- Ice cream cone
- Party hat
- Funnel
- Traffic cone
- Tip of a pencil
These real-world examples make cones one of the most recognizable 3D shapes in geometry.
The Formula for the Volume of a Cone
The volume of a cone measures how much space it takes up inside. In other words, it tells us how much material (like liquid, sand, or ice cream) can fit inside the cone.
The formula is:
V = (1/3) × π × r² × h
Where:
- V = Volume
- π (pi) ≈ 3.14159
- r = radius of the base
- h = height of the cone
Why One-Third?
The factor 1/3 exists because a cone has exactly one-third the volume of a cylinder with the same base and height. If you imagine filling a cone with water and pouring it into a cylinder with equal dimensions, it would take three cones to completely fill the cylinder.
Step-by-Step Example: How to Calculate Cone Volume
Let’s work through a practical example.
Example 1:
Find the volume of a cone with a radius of 4 cm and a height of 9 cm.
Step 1: Write the formula
V = (1/3) × π × r² × h
Step 2: Plug in the values
V = (1/3) × 3.14159 × (4²) × 9
Step 3: Square the radius
4² = 16
V = (1/3) × 3.14159 × 16 × 9
Step 4: Multiply
16 × 9 = 144
3.14159 × 144 = 452.39
V = (1/3) × 452.39
Step 5: Divide by 3
V = 150.8 cm³
Answer: The cone has a volume of approximately 150.8 cubic centimeters.
Cone vs Cylinder Volume
It helps to compare cones with cylinders because their formulas are closely related.
- Cylinder formula: V = π × r² × h
- Cone formula: V = (1/3) × π × r² × h
This means a cone has exactly one-third the volume of a cylinder with the same radius and height.
Quick Illustration
- Cylinder: r = 5 cm, h = 12 cm → V = 942.48 cm³
- Cone: r = 5 cm, h = 12 cm → V = 314.16 cm³
Yes, the cone is exactly one-third the cylinder’s volume.
Real-Life Applications of Cone Volume
The volume of a cone isn’t just a math exercise—it has real uses.
- Food industry – Calculating how much ice cream or coffee fits in a cone-shaped container.
- Construction & Architecture – Designing cone-shaped roofs, towers, or chimneys.
- Manufacturing – Funnels, packaging, and molds often use cone shapes.
- Engineering – Traffic cones, rocket tips, and machinery components are often modeled as cones.
- Storage & Transport – Measuring grain silos or tanks shaped like cones.
Cone Volume Calculator
Sometimes doing the math by hand can be slow. That’s where online cone volume calculators come in handy. You just plug in the radius and height, and the tool instantly gives you the volume.
Many free calculators are available online. For example:
FAQs About Cone Volume
1. What is the formula for the volume of a cone?
V = (1/3) × π × r² × h
2. Why is there a 1/3 in the formula?
Because the cone’s volume is exactly one-third of a cylinder with the same base and height.
3. What is the unit of cone volume?
Volume is measured in cubic units (cm³, m³, in³, etc.).
4. Can I use diameter instead of radius?
Yes, but first divide the diameter by 2 to get the radius.
5. Is cone volume used in real life?
Absolutely—architecture, food, engineering, and packaging often use cone volume calculations.
Conclusion
The volume of a cone is a simple yet powerful formula:
V = (1/3) × π × r² × h
It tells us how much space fits inside the cone. From ice cream cones to traffic cones, the concept shows up everywhere in real life. By understanding the formula, working through examples, and avoiding common mistakes, you can master cone volume with confidence.
Next time you see a cone—whether in geometry class or daily life—you’ll know exactly how to figure out how much it holds!

Leave a Reply